Category Archives: distractions

Part II: Mass of the Death Star in Episode IV

Posted on by

This is the second in a two part post where I calculate the size and mass respectively of the Death Star in Episode IV (DS1).  Estimating the mass will inform discussion about the power source of the station and other energy considerations.

Part II: Mass of DS1

As argued in Part I, I assert that the diameter of DS1 is approximately 60 km based on a self-consistent scale analysis of the station plan schematics as shown during the briefing prior to the Battle of Yavin.

A “realistic” upper limit for the mass is set if the 60 km volume of DS1 was filled with the densest (real, stable) element currently known.  This is osmium with a mass density of 2.2E4 kilograms per cubic meter.  This places the mass at 2.5E18 kg with a surface gravity of 0.05g.  A filling fraction of 10% would then place a “realistic” estimate of the upper limit at 2.5E17 kg.  Other analyses have made similar assessments using futuristic materials with some volume filling-fraction, also putting the mass somewhere around 10^18 kg assuming a radius of 160 km.

In this mass analysis, using information from the available footage from the Battle of Yavin, I find a DS1 mass of roughly 2.8E23 kg, about million times the mass of a “realistic” approximation  Any supporting superstructure would be a small perturbation on this number.  This implies a surface gravity of an astounding 448g.  To account for this, my conclusion is that DS1 has a 40 m radius sphere of (contained) quark-gluon plasma or a 55 m radius quantity of neutronium at its core.  Such materials, if converted to useful energy with an efficiency of 0.1%, would be ample to 1) provide the 2.21E32 J/shot of energy required to destroy a planet as well as 2) serve as a power source for sub-light propulsion.

Details

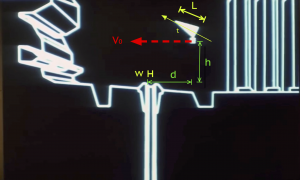
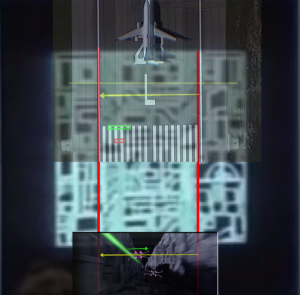
The approach here uses the information available in the schematics shown during the briefing.  The briefing displays a simulation of the battle along the trench to the exhaust port.  Again, as shown in Part I of this post, the simulation scale is self-consistent with other scales in both the schematic and the actual battle footage.  As shown in Figure 1, the proton torpedo is launched into projectile motion only under the influence of gravity.  It appears to be at rest with respect to the x-wing as it climbs at an angle of about 25 degrees.

Figure 1

Figure 2

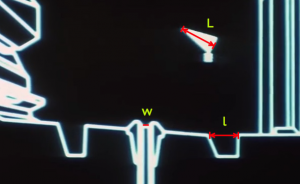
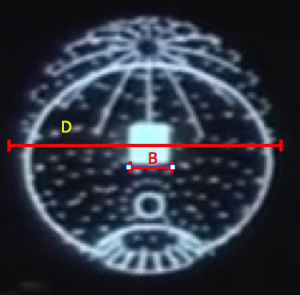
From the previous scale analysis in Part I, the distance from the port, d, and height, h, above the the port can be estimated.  They are approximately equal, h = d = 21 meters. The length of the x-wing is L = 12.5 m.  After deployment, the trajectory slightly rises and then falls into the exhaust port as shown in Figure 2.  A straightforward projectile motion calculation gives the formula for the necessary downward acceleration to follow the trajectory of an object under these conditions

a=\frac{2 V_{0}^2}{d}(\frac{h}{d}+\tan{\theta})\cos^2{\theta}\ \ \ \ (1)

Where t is the launch angle and Vo is the initial horizontal velocity of the projectile.  If we assume for simplicity that the angle \theta = 0 degrees and h = d, the formula simplifies to

a=\frac{2 V_{0}^2}{d}\ \ \ \ (2).

From the surface gravity, the mass of can be obtained, assuming Newtonian gravity,

M=\frac{a R^2}{G}\ \ \ \ (3).

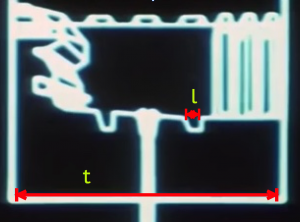
Here G = 1.67E-11 Nm/kg, the gravitational constant.  For a bombing run, let’s assume the initial speed of the projectile to be the speed of the x-wing coming down the trench.  To estimate the speed, v, of the x-wing, information from the on-board battle computers is used.  In Part I, the length of the trench leading to the exhaust port was estimated to be about x = 4.7 kilometers.  On the battle computers, the number display coincidentally starts counting down from the range of about 47000 (units not displayed).  However, from this connection I will assume that the battle computers are measuring the distance to the launch point in decimeters.  From three battle computer approach edits, shown in Clip 1 below, and using the real time length of the different edits, the speed of an x-wing along the trench is estimated to be about 214 meters/second (481 miles/hour).  This is close to the cruising speed of a typical airliner — exceptionally fast given the operating conditions, but not unphysical.  This gives a realistic 22 seconds for an x-wing to travel down the trench on a bombing run.


Using this speed and the other information, this places the surface gravity of DS1 at about 448 g (where g is the acceleration due to gravity on the surface of the earth).  DS1 would have to have a corresponding mass of 2.4E23 kg to be consistent with this.

However, it is clear that considerable liberty was taken in the above analysis and perhaps too much credibility was given to the battle simulation alone, which does not entirely match the dynamics show in the footage of the battle. Upon inspection of the footage, the proton torpedoes are clearly launched with thrust of their own at a speed greater than that of the x-wing.  A reasonable estimate might put v (torpedo) to be roughly twice the cruising speed of the x-wing.  Moreover, the torpedoes are obviously not launched a mere d = 21 meters from the port (although h = 21 is plausible), rather sufficiently far such that the port is just out of sight in the clip.  Finally, the torpedoes enter the port at an awkward angle and appear to be “sucked in.”  One might argue that there could be a heat seeking capability in the torpedo.  However, this seems unlikely.  If this were the case, then it greatly dilutes the narrative of the battle, which strongly indicates not only that the shot was very difficult but that it required the power of the Force to really be successful.  Clearly, “heat seeking missiles along with the power of the Force” is a less satisfying message.  Indeed, some have speculated that the shot could only have been made by Space Wizards.  These scenarios, and other realistic permutations, are in tension with the simulation shown in the briefing.  Based on different adjustments of the parameters v (torpedo), h, d, and th, one can tune the value of the surface gravity and mass to be just about anything.

However, if we attempt to be consistent with the battle footage, we might assume again that t=0 degrees while d = 210 m, and v (torpedo) = 2 v (x-wing) for propulsion.  The speed of the x-wing can remain the same as before at 214 m/s.  Even with this, the surface gravity will be 18g.  This still leads to a mass over 10000 times larger than the mass of a realistic superstructure.  In this case, a ball of neutronium 18 m in radius could still be contained in the center to account for this mass.

Nevertheless, my analysis is based on the following premise: the simulation indicates that the rebel analysts at least believed, based on the best information available, that a dead drop of a proton torpedo into the port, only under the influence of DS1’s gravity, was at least possible at d = h = 21 meters at the cruising speed of an x-wing flying along the trench under fire nap-of-the-earth.  Any dynamics that occurred in real time under battle conditions would ultimately need to be consistent with this.

The large intrinsic surface acceleration may seem problematic (consider tidal forces or other substantial technological complications).  However, as demonstrated repeatedly in the Star Wars universe, there already exists exquisite technology to manipulate gravity and create the appropriate artificial gravity conditions to accommodate human activities (e.g. within DS1, the x-wings, etc.) under a very wide range of activities (e.g. acceleration to hyperspace, rapid maneuvering of spacecraft, artificial gravity within spacecraft at arbitrary angles, etc.).

 

Implications for such a large mass.  

One hypothesis that would explain such a large mass would be to assume DS1 had, at its core, a substantial quantity of localized neutrinoium or quark-gluon plasma contained as an energy source.  Such a source with high energy density could be used for the purposes of powering a weapon capable of destroying a planet, as an energy source for propulsion, and other support activities.  For example, the destiny of neutronium is about 4E17 kilograms per cubic meter and a quark-gluon plasma is about 1E18 kilograms per cubic meter.  Specifically, a contained sphere of neutronium at the center of the death star of radius 55 meters would account for the calculated mass and surface gravity of DS1.

It has been estimated that approximately 2.4E32 joules of energy would be required to destroy an earth-sized planet.  If 6.7 cubic meters of neutronium (e.g. a sphere of radius 1.88 m) could be converted to useful energy with an efficiency of 0.1%, this would be sufficient to destroy a planet (assuming the supporting technology was in place).  This is using the formula

\Delta E=\epsilon\Delta m c^2\ \ \ \ (4)

where \Delta E is the useful energy extracted from a mass \Delta m with efficiency \epsilon.  The mass is converted to a volume using the density of the material.

By using the work-energy theorem, the energy required to accelerate DS1 to an arbitrary speed can be estimated.  Assuming the possibility for relativistic motion, it can be shown (left as an exerise for the reader) that the volume V of fuel of density \rho required to accelerate an object of mass M to a light-speed fraction \beta at efficiency \epsilon is given by

V=\frac{1}{\sqrt{1-\beta^2}}\left(\frac{M}{\epsilon\rho}\right)\ \ \ \ (5).

This does not account for the loss of mass as the fuel is used, so represents an upper limit.  For example, to accelerate DS1 with M = 2.4E23 kg from rest to 0.1% the speed of light (0.001 c) would require about 296 cubic meters of neutronium (a sphere of radius 4.1 m).

From this, one concludes that the propulsion system may be the largest energy consideration rather than the primary weapon.  For example, consider DS1 enters our solar system from hyperspace (whose energetics are not considered here) and found itself near the orbit of mars.  It would take two days for it to travel to earth at 0.001 c.

 

Part I: Size of the Death Star in Episode IV

Posted on by

This is the first in a two part post where I calculate the size and mass respectively of the Death Star in Episode IV (DS1).  At the end of Part II I will discuss thoughts about the energy source of DS1.

Part I: Size of DS1

Conventional wisdom from multiple sources places the size of DS1 to about 100-160 km in diameter.  Based on an analysis of the station’s plans acquired by the Rebels, I estimate that the diameter of DS1 is 60 kilometers, not 100 km to 160 km.  To bolster the case, this scale is compared to other scales for self-consistency, such as the width of the trench leading to the exhaust port in the Battle of Yavin. Part II of the post will focus on the mass of DS1 using related methods.

To estimate the size of DS1, I will begin with the given length scale of the exhaust port w = 2 m.  This information was provided in the briefing prior to the Battle of Yavin where the battle strategy and DS1 schematics are presented.  This scale, when applied to Figure 1, is consistent with the accepted length of an x-wing L = 12.5 m.  I assume that the x-wing has an equal wingspan (there does not seem to be consistent values available).  I am also assuming that the “small, one-man fighter” referred to in the briefing is an x-wing, not a y-wing.  The x-wing is a smaller, newer model than the y-wing and it is natural to take that as the template.  The self-consistent length scales of w and L will establish the length calibration for the rest of the analysis.

Figure 1: A close up view of the exhaust port chamber during final phase of the bombing run.  The port width is given as w = 2 m.  The length of the x-wing is L = 12.5 m.  The forward hole, of length l, is then determined to be about 10 m.

From this, I extract the length of the smaller forward hole in Figure 1 to be approximately l = 10 m.

Figure 2: As the plans zoom out, a larger view of the exhaust port chamber of width t = 186 m.  The first hole is shown with width l = 10 m.  The scale of width l was determined based on information in Figure 1.  The width of t was determined based on the scale of l.

Using l as a calibration, this establishes the exhaust port chamber in Figure 2 to be approximately t = 186 m.

In Figure 3a and Figure 3b, circles of different radii were overlaid on the battle plans until a good match for the radius was established.  Care was taken to have the sphere’s osculate the given curvature and to center the radial line down the exhaust conduit.  From here, the size of the exhaust port chamber, of width t, was used as a calibration to approximate the diameter of DS1 as D = 60 km (red).  Several other circles are show in Figure 3 to demonstrate that this estimation is sensible: 160 km (purple), 100 km (black), and 30 km (blue).  It is clear that a diameter of 160 km is definitely not consistent with station’s schematics.  A diameter of 100 km is not wildly off, but is clearly systematically large across the range over the given arc length.  30 km is clearly too small.

While a diameter of 60 km may seem modest in comparison to the previously estimated 100 km to 160 km range, an appropriately scaled image of New York City is overlaid in Figure 4 to illustrate the magnitude of this systems in real-world terms; even a sphere of 60 km (red) is an obscenely large space station, considering this is only the diameter — more than adequate to remain consistentwith existing canon.  The size of the main ring of the LHC (8.6 km) is overlaid in light blue, also for scale.

Figure 3a (to the right of the exhaust port chamber): As the plans zoom out further, the exhaust port chamber of width t = 186 m is shown with the curvature of DS1 (the square blob is the proton torpedo that has entered the port).  The scale of t was determined based on information in Figure 2.  Several circles with calibrated diameters based on the scales set in Figures 1 and 2 are shown.  The 60 km diameter circle in red is arguably the best match to the curvature.  Care was taken to match the point of contact of the circles to a common central location along the radial port.

Figure 3b (to the left of the exhaust port chamber): The same idea as Figure 3a.  The 60 km diameter is still arguably the best match, although is a little shy on this side. The 100 km diameter, the next best candidate, is shooting higher than the 60 km is shooting low. Since an exact mathematical fit wasn’t performed, the expected radius is probably a bit higher than 60 km, but significantly lower than 100 km.

 

 

Figure 4: A 60 km diameter circle in red (with yellow diameter indicator) shown overlaid on a Google Earth image of the greater New York City region.  The blue ring is an overlay of the scale of the Large Hadron Collider at CERN (about 8.5 km in diameter) — note the blue ring is not a scaled representation of the main weapon!  The main message here is that a 60 km station, although smaller than the accepted 100-150 km, is still freakin’ HUGE.  At this scale, there is only a rather modest indication of the massive urban infrastructure associated with New York City.

As another check on self-consistency, the diameter D is then used to calibrate the successive zooms on the station schematics, as shown in Figures 5 and 6.  The length B = 10 km is the width of the zoom patch from Figure 5, X = 4.7 km is the length of the trench run, and b = 134 m is the width of one trench sector. From Figure 6, the width of the trench is estimated to be b’ = 60 m, able to accommodate roughly five x-wing fighters lined wingtip-to-wingtip.  This indicates that the zoom factor is about 1000x in the briefing.

Figure 7 is a busy plot.  It overlays several accurately scaled images over the 60 m trench, shown with two parallel red lines, to reinforce plausibility.  Starting from the top: an airport runway with a 737 ready for takeoff (wingspan 34 m); a 100 m-wide yellow calibration line; a 60 m-wide yellow calibration line; the widths of an x-wing (green, Wx = 12.5 m, where I’ve assumed the wingspan is about the same as the length — there does not seem to be a consensus online; I’ve seen the value quoted to be 10.9 m, but it isn’t well-sourced) and tie fighter (red, 6.34 m); and a scaled image from footage of two x-wings flying in formation, with a yellow 60 m calibration line as well as a calibrated green arrow placed over the nearer one to indicate 12.5 m.  As predicted, about five x-wings could fit across based on the still image.  Also from this, the depth of the trench is estimated to also be 60 m.  The scales are all quite reasonable and consistent. It is worth noting that if the station were 100 km, the next possible sensible fit to the arc length in Figure 3, the width of the trench would be about 100 m, twice the current scale.  This would not be consistent with either the visuals from the battle footage or the airport runway scales.

In short, while there is certainly worthy critique of this work, I argue that, after a reasonably careful analysis of the stolen plans for DS1, all scales paint a self-consistent picture that the diameter of DS1 is very close to 60 km.

Figure 5: A zoom-out of DS1 in the briefing based on the stolen battle plans.  D = 60 km is the diameter and B = 10 km is the width of the patch in the region of interest near the exhaust port.

Figure 6: A zoom in in the region of interest patch near the exhaust port channel (see Figure 5) with B = 10 km.  the channel itself is about X = 4.7 km long.  The width of the channel is about b = 134 m.  Inset is a further zoom of the insertion point along the channel.  Width of the channel itself is about b’ = 60 m.

Figure 7: A zoom of the insertion point along the channel for the bombing run.  Several elements are overplayed for a sense of scale and for consistency comparisons.  The red parallel lines represent the left and right edges of the channel.  From the top of the figure is a 737 with a wing span of 34 m.  The 737 is on a runway (at SFO).  Down from the 737 is a  yellow line that represents 100 m.  This would be the width of the channel if D = 100 km, which is clearly much too large based on the battle plans.  The next horizontal yellow arrow is the 60 m width based on the scales assumed with D = 60 m.  Next down, embedded in the vertical lines of the runway: a green block representing the width of an x-wing and a red block representing the width of a tie fighter.  Finally, at the bottom is a shot from the battle footage.  It has been scaled so the edges of the walls match the width of the channel (shown as a horizontal yellow arrow).  The width of the near x-wing is shown with a green horizontal arrow, which matches the expected scale of an x-wing.

 

Solve Any Number Sequence Problem (Cheap Shot)

Posted on by

Number sequence puzzles are a problem solving staple. There are obvious ones, obscure ones, and famous ones like the Fibonacci sequence. I assert that given a few numbers (say 5 or 6) in a sequence and asked to identify “what is the next number?” there is a way to solve it that won’t generally involve the intended solution, but will nevertheless aways be right.  But it is sort of cheating. No, take that back. It is cheating.

The trick is to find the (first appearance of the) sequence you seek in the digits of pi or any other transcendental number like e, phi, or pick your favorite.  You can then read off the remaining digits using some convenient grouping to fill out the sequence to arbitrarily large values of necessary.  Frequently, unless you have pi memorized to hundreds of thousands, millions, even billions of digits, this will require a program or online resource of some kind to find the sequence in the digits of pi.

Let’s do some examples.  Take a few number series puzzles from dailybrainteaser one of many such fun puzzle sites:

What is the next number in this series?
6, 14, 36, 98, 276, ?

First, we look for the pattern 6143698276 in pi using, The Pi-Search Page, or Irrational Numbers Search Engine.  The former does a fast, as you type, search over the first 200 million digits while the later does a deeper search out to 2 billion digits (these are just a couple of many sites available).  As any small child can see, 6143698276 appears at the 1,962,082,153th digit of pi.  A few of the digits after that look like: 614369827631848334.  One can then casually claim something like: “the next number in the sequence 6, 14, 36, 98, 276 is 318 where 318 is (obviously) the next three digits after 6143698276 starting at the 1,962,082,153th digit of pi.  Bam!”  Mike drop.  No argument.

As the given sequence gets longer, the less likely one will find the sequence in a transcendental search engine assuming such numbers are essentially a random distribution.  For example, the sequence 6143698276 doesn’t occur in the first two billion digits of e or sqrt(2).

Here’s another:

What Comes next in sequence
1 , 4 , 5 , 6 , 7 , 9 , 11 ?

This one’s easy because it is relatively short.  The pattern 14567911 appears at the 64,362,285th digit of pi.  The few digits after it are 1456791122892. So, with great confidence, you can say “the sequence is obviously 1, 4, 5, 6, 7, 9, 11, 22.”  Repeat argument above.  End conversation awkwardly.

I appreciate this is quite gimmick-y.  One can invent any number of arbitrary solutions to these sequence puzzles.  Even for this approach, there will be multiple perfectly correct solutions, even just using pi alone.  For example, in our second example above, 14567911 appears an infinite number of times in pi.   Puzzles of this kind optimally involve a very specific elegant solution that uses your Puzzler.  Nevertheless, this approach is amusing for the first couple times, lets you get your geek out, and can at least temporarily distract family and friends while you really try to solve the puzzle.

Wednesday Mourning

Posted on by

Even after just over two weeks, I’m still not in an emotional or intellectual state of mind to discuss the details of the 2016 presidential election.  I’m profoundly angry and disappointed, even depressed, with the outcome Tuesday, November 8, 2016. The world feels like a darker place. If I’m feeling the way I do, I can only imagine how others, who have much more at stake than I do, must feel.

Regarding any discussion of the election in my personal life, I shut every casual family conversation down.  Every hallway discussion at work.  Every Sunday morning pundit.   I can’t listen to any tabloid media at all on any topic: no Huffington Post;  no Facebook feeds;  no clever memes;  no MSNBC;  no CNN;  no SNL; no John Oliver; no Steven Colbert; no FOX, no political comedy.  You get the picture.  Also, in an act of awfulness, I cut out any other reputable political news sources except for actual useful, hard information coming from the likes of NPR, NYT, and the Washington Post.  In all cases, no opinions or speculation perpetuated by the punditocracy are allowed.  I can’t.  It all seems so transparently stupid now.

If I seem out of touch, forgive me. If Hawaii has already seceded and Alaska was invaded by Iceland, I’m probably a month behind these developments. If a recount or unfaithful elector made Jill Stein president, I’m probably too consumed with teaching my courses to care.  I currently rely on my wife to tell me if we nuke Canada or make Bill Cosby the Secretary of Education, otherwise I’m out.  Some have told me this decoupling is irresponsible.  They are right. Dear colleagues: yes, I will join the fight again.  But I can’t do it now. Not yet.  I need to mourn.

Come January 2021, I can only hope President Obama will be sworn into office as the first female black president.

Gray Hair Issue in A Rose For Emily

Posted on by

A Rose for Emily is a classic short story by William Faulkner.  There are spoilers here, so if you haven’t read it, I suggest doing so before proceeding.  It is a fun, quick read.  If you want, you can read the plot summary on the Wikipedia page.  I will identify the plot points I think are important for my analysis, but will assume the reader is familiar with the story.

SPOILER ALERT

Some technical observations

The story has many layers to it, technical, literary, and symbolic.  For example, on a technical level, Faulkner mostly uses the interesting first person plural point of view.  That is, the story is narrated abstractly by “the town” that refers to itself as “we,” yet using the tone as if it were an individual.  That is, “we” thinks of itself as a single person.  Perhaps this is meant to imply that a single person from the town is telling the story as an old yarn for a passerby on behalf of the rest?  But we are never told who this narrator is or what their actual role is in the story.  They seem to be in on every detail of the plot in an omniscient way that no single person could realistically know.  In any case, this point of view does add a layer of abstraction (for me, anyway).

Another technical twist is how Faulkner really gets us turned around with the timeline.  This type of non-linear plot seems natural in the telling (as if it were told from the collective memory of the entire town).  In fact, the timeline has even been analyzed by computer algorithms to find inconsistencies.

Summary and question

The story is about a woman who killed her lover years ago and has been sleeping with his dead body.  Early in the story it is obvious she killed someone.  Eventually the reader can figure out it is Homer Barron, her lover.  The climax is the realization she has been sleeping with the body.

My question is: how recently had she slept with the body?  My assumption, since I first read the story as a youngster, was that she had been sleeping in that bed with him right up until her death.  But that isn’t consistent with the information in the story.  My conclusion:  Although she died when she was seventy-four, she must have stopped sleeping with the body when she was in her mid-thrities.  What is my reasoning?

A little preamble

Most of the time in the story, Faulkner is just playing with us.  He wants the the reader to believe the town folks are just daft and couldn’t figure out there was a body in the house and that she killed someone (or was about to, depending on where we are on timeline).  Later, when it is mentioned that Homer Barron vanished, we as the reader think we have it all figured out.  You could see that coming from a mile away!  How very clever we are!  In fact, you start to question the competence of Faulkner because it looks like he’s is going to end with a softball murder mystery.  Sure the writing is pretty like poetry, but couldn’t he have had a better, less cliche, plot? 

You start to question the competence of Faulkner because it looks like he’s is going to end with a softball murder mystery.

The clues and my case

The cracks of my established assumptions start in Section V after she dies:

“Already we knew that there was one room in that region above stairs which no one had seen in forty years, and which would have to be forced”

The key terms are “no one had seen in forty years” and “had to be forced.”  Taken literally, “no one” includes her.  That the door had to be forced emphasizes the door wasn’t just locked, but stuck because of neglect.  Also, there is no mention of a key.  If Faulkner wanted to emphasize that she could have, in principle, been in the room over the intervening forty ears, he only needed to add the adjective “locked” to “door.”  But he didn’t. Then they bust it down.  Since she died at seventy-four, going forty years back, she had to be about thirty-four since being in that room.

When they bust into the room they find the body of Homer Barron on a decrepit bed.  The piece finishes with the famous climax:

“Then we noticed that in the second pillow was the indentation of a head. One of us lifted something from it, and leaning forward, that faint and invisible dust dry and acrid in the nostrils, we saw a long strand of iron-gray hair.

Yikes!  It isn’t a murder mystery at all.  We realize that we were supposed to figure out early in the story that she murdered him.  It was a ploy to lead us into a false sense of security.  No, the mystery isn’t that she just murdered him, but had been sleeping with him, perhaps even engaging in necrophilia.  Ew!

Right before the climax, we get a description of the pillow:

 “and upon him and upon the pillow beside him lay that even coating of the patient and biding dust.”

Notice that the second pillow, with the iron gray hair, was as dusty as the room. I assert it also hasn’t been used for forty years.  Indeed, these are the exact words one would use to describe a pillow that hadn’t been used in decades.

All this implies she not only had to be about thrirty-four when she was last in the room, but it was also implies that this was the last time she slept with the body.

Timeline of gray hair development?

Earlier in Section III, he states

“‘I want some poison,’ she said to the druggist. She was over thirty…”

So she must kill Homer when she is older than thirty.

In Section IV Faulkner describes the evolution of her gray hair and the passage of time:

“When we next saw Miss Emily, she had grown fat and her hair was turning gray. During the next few years it grew grayer and grayer until it attained an even pepper-and-salt iron-gray, when it ceased turning. Up to the day of her death at seventy-four it was still that vigorous iron-gray…”

The paragraph prior describes the period time right after her lover, Homer Barron, disappears.  Then “some time” passes.  Then they “next saw Miss Emily” and her hair is graying and turns grayer and grayer over the next “few years” and it seems to saturate to iron gray at this time.  Then she does the china-painting when she was about forty, presumably when her hair was already saturated gray.  Then there is an extended period when they don’t see her.  When she dies at age seventy-four, she still has the iron gray hair.

 It makes you wonder if her early graying had something to do with the stresses of engaging in necrophilia.

So, the timeline of the gray hair on the pillow (as I now interpret it) goes something like this:

  1. “Over thirty:” kills Homer with arsenic, hides the body in the house (smell had to start around here, right?)
  2. Early-thrities: the town folk next see her again, hair turning gray
  3. Mid-thirties: “the next few years” hair turns grayer and grayer, saturating in an iron gray color
  4. “About forty:” Starts china-painting, hair already iron gray
  5. Mid-Sixties: they try and collect taxes, “vanquished them, horse and foot, just as she had vanquished their fathers thirty years before about the smell”
  6. Forties through seventies: seen occasionally in the window
  7. Seventy-four: she dies, room is busted open after being closed for forty years, iron-gray hair is next to pillow, bringing us to somewhere around (3) when she last left the iron-gray hair.

Anyway, this is very different from my image of her sleeping with the body up to the age of seventy-four.  The story implies that she last slept with the body as a woman around age thirty-four, leaving the iron-gray strand on the pillow.  After that, she sealed the room for forty years before her secret was discovered by the towns people after she died.

It makes you wonder if her early graying had something to do with the stresses of engaging in necrophilia.

Wrap up

Perhaps all this theory is well known amongst Faulkner scholars and high school English teachers, but I had fun teasing out these clues.

I think I have made a pretty good case, based on the text itself, that she hadn’t slept with the body for about forty years before her death. I’m not sure “if” or “how” this changes any of the story’s message.  Perhaps it implies she herself stopped clinging to the past long ago, but was still willing to let it fester in the sad recesses of her mind.

If you assume she had been sleeping the body until her death, you have to add extra information not provided: perhaps there was a key, perhaps the towns folk kicked up dust and it landed on the pillow, perhaps she lay softly enough on the pillow to not disturb the dust, perhaps by “no one” it means “no one but her.”

Faulkner was more about symbology of the Old South than murder mysteries.  My observations may highlight unimportant details that aren’t important for the basic message.  Still, if my hypothesis holds together, I have another question: why did she stop sleeping with the body when she was thirty four?

The Best Nest

Posted on by
A0742B3C-042C-4203-B8E2-CD22B81D2971

The Best Nest by P.D. Eastman

 

The classic children’s book The Best Nest by children’s author P.D. Eastman, published in 1968, is one of the books that really sticks with me from my childhood.

I recall my mom reading it to me when I was about four or five. I’ve read it to my kids for years and my four-year-olds particularly adore it. It is the simple story of how a mama and papa bird go through a series of misadventures in an effort to find a new home, only to discover that their original home was really the best one after all. We find out at the end that the mama bird was ready to lay an egg and the whole effort was driven by her motherly instinct to find a safe space for her baby. It is sappy, and reinforces certain gender stereotypes, but is ultimately good-natured. While simple, it does follow the classic hero’s journey. After hardship and adventure, you find your way back to where you started as changed person (or bird, in this case), now wiser to the ways of the world (like not to nest in bell towers). When we got it for my kids years ago, I had instant flashbacks with the artwork, recalling fixations I’d had with certain details that, as an adult, I would never have noticed: the way the straw stuck out in their mouths, the particular hat the mama bird wore, the particular angle and character of the rain that came down on the papa bird at the end. All of it jumped out again.

 

879ABDAA-6F12-450D-A1CF-AB83334CA602

The church in the town featured in The Best Nest

One of the big turning points in the story is when the birds find this wonderful space for their nest. It is huge. It has all sorts of great views of the area. The mother bird thinks it is the best place. However, we, the reader, know that something will go terribly wrong: the space is really a bell tower for a church. The papa bird goes out to find new materials for their nest while the mama sets up shop. Well, sure enough, a funky beatnik proto-hippy guy named Mr. Parker, comes to the church and rings the hell out of that bell like he has no other outlet for his life’s frustrations.  The guy clearly loves his job. The papa bird comes back to find the place littered with bird feathers and no mama bird. He fears the worst and goes on a quest to find her.

Oberlander R.D. #1 Waldoboro, Ma...

Oberlander, R.D. #1, Waldoboro, Ma…

Before they find the bell tower, they look in other places for a new nest. One of the potential nests is a mailbox. Now, as I mentioned, as a kid I had particular fixations in details I would never had seen as an adult; conversely, in reading it to my children, I also found details I would never have found as a kid.  For example, one of the reasons they decided not to pick the mailbox is that, while they were checking it out, a mailman comes by and puts some mail into the mailbox.  Definitely not an ideal space for a pair of birds.

However, the piece of mail has an address on it (upside down in the text of the book):

…Oberlander
R.D. #1
Waldoboro, Ma…
Circa 2016, there is indeed an [Old] Road 1 in Waldoboro, Maine.  There is also an Oberlander family name that appears in that town’s older records.  That’s sort of neat.  Naturally, using Google Streeview, I wandered around to see if I could find the church where the bell tower was.  While not definitive, I have two candidates.  Sure, these churches are pretty generic shapes for the area.  Nevertheless, with a specific town to focus on, you can be pretty sure it must be one of two churches, or a composite, that P.D. used as a template.  He could have also just made something up from memory or imagination.
The first one, Broad Bay Congregational Church, has the correct weathervane, the correct three-window structure, a circular region in the middle, and an obvious bell tower.  It also has a front that is roughly consistent with the drawing, although obviously updated (e.g. it has two windows on each side of the door).
Waldoboro Broad Bay Congregational Church, 941 Main St, Waldoboro, Maine)

Waldoboro Broad Bay Congregational Church 941 Main St, Waldoboro, Maine

The second one, Waldoboro United Methodist Church, also has the three window configuration in the side, has similar slats near the bell tower as the drawing in the story (the slats were one of the weirdly specific things I fixated on as a child), and a pointy tower that resembles the one in the drawing.  But it does not have the right window configuration, the weathervane, nor the circular slats.
Waldoboro United Methodist Church (side view), 85 Friendship Street (Route 220), Waldoboro, Maine)

Waldoboro United Methodist Church (side view) 85 Friendship Street (Route 220), Waldoboro, Maine

Waldoboro United Methodist Church (front view), 85 Friendship Street (Route 220), Waldoboro, Maine.

Waldoboro United Methodist Church (front view), 85 Friendship Street (Route 220), Waldoboro, Maine.

My hunch is that the first one, Broad Bay Congregational Church, is the one in the story.  I suspect that during the time since P.D. Eastman wrote the story (circa 1968),  it has had a few upgrades.
But, as I said earlier, these are very common generic “Protestant-style” East Coast churches.  The story might have nothing to do with these specific churches.
Anyway, I had fun with this little distraction.  If anyone knows more about this Easter egg planted by P.D. Eastman, about any connection he may have had to the Waldoboro region, or the reason he might have picked “Oberlander” for the recipient of the letter on R.D #1, I’d love to hear about it.

Reading Audiobooks

Posted on by

If you listened to an audiobook is it responsible to say in conversation that you “read the book” without qualifying that it was an audiobook? Does listening to an audiobook constitute “reading a book”? The answer is “yes,” although this will require some explanation. The question sounds strange because I just said that you listened to it, and didn’t read it, didn’t I? And “reading” isn’t “listening” so how can listening to an audiobook allow one to claim one has “read the book”? I think some of this discussion is motivated by my own enjoyment of audiobooks in the face of those who can only be called “reading snobs” who dogmatically believe that books can only be “properly” processed one way: via the written text and with one’s eyes. There also may be a perception that listening to an audiobook is somehow easier or intellectually lighter than reading the text of a book. To this I say: try listening to an audiobook sometime. In my experience, audiobooks can be very intellectually satisfying and may even be a heavier cognitive load than reading text because your eyes are free to roam and process independent information. This forces no small measure of mental discipline to remain focused and engaged but still function (e.g. if you are walking or driving).

I just listened to David Brin’s excellent Uplift War on audiobook, and unapologetically declare to the world that I “read the book.” For full disclosure, I’ve also read Martian Chronicles by Ray Bradbury, all three Hunger Games novels by Suzanne Collins, Sara Gruen’s Water for Elephants, Neverwhere by Neil Gaiman, Packing for Mars by Mary Roach, and Letters to a Young Contrarian by Christopher Hitchens, amongst others. All on audiobook. From a social point of view, if you and I got together to discuss these works, my experience of them would be such that you would not be able to determine by our conversation if I listened to it or physically read the words on a page. In this sense, I can responsibly claim to have “read the book” even if my eyes never looked at the words. That is, using Brin’s work as an example, unless you asked me to spell the names “Uthacalthing”, “Tymbrimi”, or “Athaclena” (which I did not know how to spell until I looked them up just now) — but then I’d ask you to pronounce them and we’d be even.

There are two elements to consider: 1) reading as a physical method of information transfer and 2) reading as an intellectual exercise involving mental content absorption. Both senses of the term “read” are used regularly and interchangeably and we will need to remind ourselves what is really important. Certainly a quick scan of the dictionary (and one’s own experience) demonstrates the word “read” in the English language is used in many different ways. One of those ways is the specific biomechanical method of scanning physical symbols with one’s eyes. However, that same exact sense of the term also describes the methods of a person using their fingers to process braille symbols. Feeling something is biomechanically and mentally nothing like seeing it, but we are still comfortable using “read” in that context, allowing “read” to span the senses because it accomplishes the same intellectual function as reading symbols with one’s eyes. This is important. Other grammatically correct uses of the word “read” also include a broader defintions involving generalized mental information processing and experiences. Phrases like “I read you loud and clear” (e.g. for a radio transmission, when listening), “reading a situation” (assessing the subtleties of a situation, including your own intellect), performing “a cold reading” (another situational assessment tool used by magicians and “psychics” involving both mental acuity and all the senses), “I’m taking a sensor reading” (to describe a technology-based data acquisition process), and so on. For the primary defintions of “read” Merriam-Webster is actually rather non-committal about the method and focuses on generic sensory information processing, definitely emphasizing the written text and braille, but not insisting upon it, allowing for many other modes.

In this spirit, let’s examine what people mean in conversation about a work of fiction when they say “I read the book” or ask “did you read the book?” Let’s assume we are dealing with educated adults and not people just learning to read text. I assert that what people universally mean by the question “did you read the book?” is “did you intellectually and emotionally absorb and process the content of the work that was created by the author?” If I listened to an unabridged audiobook in an active and engaged way, I think the answer is unambiguously “yes, I read the book.” Sure, from a methodological point of view, I did not literally (literally) read the physical text on the page with my eyes. However, this is not usually the important part of the novel, nor is it generally the important part of “reading novels.” The mechanics of looking at words is not typically the essential experience of reading books. The important part is mentally absorbing the content of the work, which is actually the core definition of the word “read” to begin with. Why would anyone care about your particular mode of information transfer? What they (hopefully!) care about is the experience you had intellectually and emotionally absorbing the content and your ability to discuss that experience in a way that transcends the transfer mode.

Do all books lend themselves to this audio mode of reading? No. Obviously not. Exceptions include works that rely directly on the shapes of words or encoding extra information in the precise layout of the text, font, or presentation. If the work involves lots of pictures, illustrations, data, or equations, audiobooks are not going to work very well. But the bulk of modern fiction lends itself wonderfully to audiobooks as does much non-fiction. Like so many other things in life, one needs to account for individual cases. Also, this equivocation is not appropriate for people (e.g. children) learning to read symbols on the page. An audio experience is not an adequate substitute for that kind of information processing during those fragile formative years. This argument is directed at people who have mastered both reading and listening and are educated adults.

To be clear, I’m not suggesting we follow the reductio ad absurdum path and call all forms of information processing “reading” in every context for all conversations. That is a straw man of my argument. I’m merely suggesting that actively listening to an unabridged audiobook can, for social and intellectual purposes, be considered “reading a book” based on the sense of the word “read” one uses in conversations of that kind. There is nothing more I would gain from a content or entertainment perspective by re-reading the book using physical text in order to “elevate” myself to “having read the [text of] the book.” Nor am I suggesting that we substitute listening to audiobooks in place of reading text in schools, although I do think both forms could be used in tandem or parallel. As mentioned above, reading symbols is obviously a critical core skill that must be developed actively and early. But, once mastered, I assert that the two forms of information processing, listening and reading, blur into each other and naturally compliment each other. And I’m certainly not dismissing the process of reading physical text as an intellectual and worthy exercise. I still read many books this way. Also, I’m not claiming that there is absolutely no difference cognitively between how the brain processes words and symbols and how it processes sounds. But I do think that in the case of listening to a word-for-word reading of unabridged audiobooks, and for the educated person who has mastered both reading and listening, the audio experience and the reading experience merge for all practical purposes into a common intellectual experience with only minor variations that do not favor systematically one mode over another except by the taste of the user.

A couple tangential examples, that inform the discussion. A formally trained and competent musician can look at a piece of written music and, for all practical purposes, “listen” to it by reading it with their eyes. The audio performance itself, of course, also has aesthetic value for that musician. But it would probably be appropriate for someone in that position to say, in either context, that they “listened” or “heard” the piece even if it merely involved reading the sheet music. Indeed, musicians who can read written music like that do refer to reading sheet music as having “heard” or having “listened” to the piece. In contrast, many bands we worship refer to “writing” music for their albums. However, rarely are any notes or music written down in any formal sense. Many rock/pop bands “write” music by playing it and piecing together sections into things than sound nice after editing (if they are lucky). Later, some music grad student, desperate to eat and pay rent, will be hired by a company to transcribe the sounds on the album into written notes, so other people without ear training can also play the songs; but that isn’t the way the band itself usually “writes” music — unless you are Yes or Dream Theater. If the Rolling Stones speak of “writing” music for a new album, they almost certainly mean a wanton, drug-infused geriatric orgy in the Caribbean that might have involved Keith Richards bringing his guitar. But the term “writing music” is still used. We can also reverse the situation and look at words on a page that were meant to be spoken out loud, such as plays. Take Shakespeare. Certainly the stage play is considered a respectable form of literary art and Shakespeare is arguably the greatest writer of the English language. But the plays he wrote were meant, designed, crafted to be read aloud and listened to. Yet we read them. Can you still read Shakespeare and claim to have experienced the work in an intellectually satisfying way and be conversational about it? Obviously. Does the stage work bring the work to life in a different way? Clearly.

Also, reading words on a page is not itself a magic recipe for intellectual absorption. Reading text can be pathologically passive if one is not actively engaged, and does not imply extra profound and deep understanding. Let me give an example from my own experience in the classroom. I tell students to “read chapter 10” from the text. And, indeed some do look at it with their eyes and the words are streamed through their thinking in some fashion. But in many cases no cognitive engagement has occurred. By speaking to them, I can tell that they did not, in fact, “read” the text as I meant the term “read.” In this context, “read” did not necessarily literally mean merely looking at the words, although it might conveniently involve that biomechanical process. I really just wanted them to come to class having processed and understood the material provided in the book by whatever means necessary. If that involves listening to the audiobook, it just doesn’t matter to me (although, good luck learning quantum mechanics from an audiobook).

Does watching a movie adaptation of a book count as “reading the book?” Not in my opinion. Putting audiobooks in the same category as movie interpretation of books is missing the point. I claim the unabridged audiobook is not, fundamentally, a different medium than the original work — not any different than the braille modes of reading that are considered “legitimate” reading. When we read books using the written word we are, in fact, “speaking” the words to ourselves in our head anyway exactly in the way the book is being read in an audiobook. A movie, even one adapted to be nearly identical to the book, is usually abridged and has been altered from the original work in fundamentally different ways. Moreover, one is not required to visualize the plot and characters in the same way as one does in reading text or listening to a reading of text.

I am not judging all these different modes or ranking them. They each serve their purpose and can give pleasure and intellectual stimulation in their own way. But I argue that, under many common situations, listening to audiobooks accomplishes the same social and intellectual function as reading text and can thus be responsibly declared a form of “reading the book.”

Mathematica One-Liner Competition 2012

Posted on by

Decided to enter Wolfram’s Mathematica One-Liner Competition 2012:  “What can you do with one line of code?”  That is, in under 140 characters (making it tweetable).  Why, a Particle Zoo Calliope, of course! My entry (only slightly modified from that submitted):

SectorChart[
 Button[{1, p[#, s]},
 EmitSound@Sound@SoundNote@{2 p[#, s], Floor@p[#, "Mass"]^.3}]
/.s -> "Spin" & /@ ParticleData[] /. p -> ParticleData]

W00t! Received an Honorable Mention! (the competition was fierce, lots of good one-liners). Give it a try below. You will need the free Mathematica CDF plugin installed. A figure will be generated. It is a musical instrument. Click on different locations on the figure to play different intervals. The first click is sometimes a bit awkward/slow, but after that it should play in real time.


Description:
A sector plot is generated based on the spin of all the known elementary particles (quarks, leptons, and gauge bosons) and the hadronic bound states (bayrons and mesons). The length of the tine on the sector plot is proportional to the particle’s intrinsic spin. There are around 1000 particles in the database. When you click on one of the sectors, representing a particle, two tones are played based on the spin and the mass of that particle. The mapping from values to notes is arbitrary, but selected to be “listenable.” I take two times the particle’s spin as one note and the integer part of the particle’s mass to the 0.3 as the second (this was selected by trial and error to give a reasonable range of tones for the full particle mass spectrum). A value of “0” is considered middle C and each integer above and below is a half-step.